Graphing Circles using Standard Form

Slide2Section 10.1 – The Circle

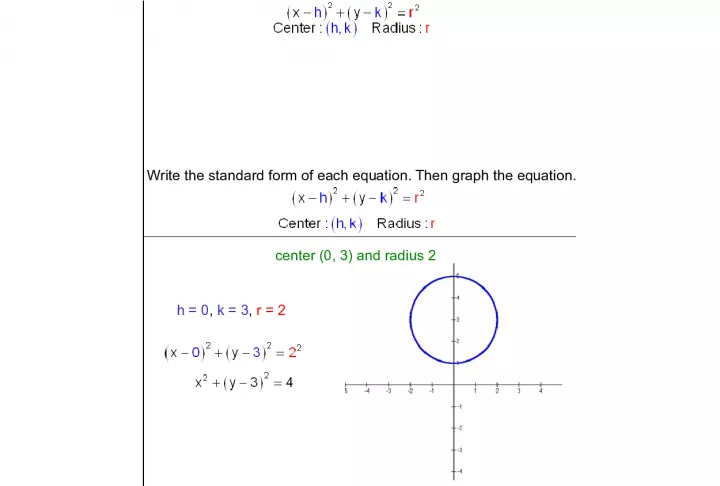
Slide3write the standard form of each equation. then graph the equation.center (0, 3) and radius 2 h = 0 ,  k = 3 ,  r = 2

Slide4write the standard form of each equation. then graph the equation.center (-1, -5) and radius 3 h = -1 ,  k = -5 ,  r = 3

Slide5write the standard form of each equation. then graph the equation.

Slide6write the standard form of each equation. then graph the equation.

Slide7write the standard form of each equation. then graph the equation.

Slide11find the equation of the circle with center (8, -9) and passesthrough the point (21, 22).

Slide12find the equation of the circle with center (-13, 42) and passesthrough the origin

Slide13find the equation of the circle whose endpoints of a diameterare (11, 18) and (-13, -20) Center is the midpoint of the diameter Radius uses distance formula

Slide14find the equation of the circle tangent to the y-axis andcenter of (-8, -7). C r = 8

Slide15find the equation of the circle whose center is in the firstquadrant, and is tangent to x = -3, x = -5, and the x-axis x x r = 4

Slide16Section 10.2 – The ParabolaVertex:  ( h, k ) Opens Left/Right Opens Up/Down Vertex:  ( h, k ) Focus: Focus: Directrix: Directrix: Axis of Sym: Axis of Sym:

Slide17Vp 2p 2p F p Directrix

Slide18Vp 2p 2p F p Directrix

Slide19Given the equationa) Write the equation in standard form V F b) Provide the appropriate     information. Focus:  (0, 2) Vertex:  (0, 0) Directrix:  y = -2 Axis of Sym:  x = 0 c) Graph the equation

Slide20Given the equationa) Write the equation in standard form

Slide21Given the equationa) Write the equation in standard form V F b) Provide the appropriate     information. Focus:  (4, 2) Vertex:  (2, 2) Directrix:  x = 0 Axis of Sym:  y = 2 c) Graph the equation

Slide22Given the equationa) Write the equation in standard form

Slide23Given the equationa) Write the equation in standard form V F b) Provide the appropriate     information. Focus:  (3, 0) Vertex:  (3, 2) Directrix:  y = 4 Axis of Sym:  x = 3 c) Graph the equation

Slide24write the equation of the parabola with focus at (2, 2)and directrix x = 4 F V

Slide25write the equation of the parabola with v(-1, -3) and F(-1, -6)V F

Slide26write the equation of the parabola with axis of symmetry y = 2,directrix x = 4, and p = -3 V F

Slide27Section 10.3 – The Ellipsea  >  b a  – semi-major axis b  – semi-minor axis C( h ,  k ) V1( h   + a ,  k ), V2( h   – a ,  k ) F1 ( h   + c ,  k ),  F2 ( h   – c ,  k ) C( h ,  k ) V1( h ,  k  + a ), V2( h ,  k  – a ) F1 ( h ,  k   + c ),  F2 ( h ,  k  – c )

Slide28CV1 V2 a a b b F1 F2 c c C(1, 4) V(1, -1), (1, 9) F(1, 0), (1, 8)

Slide29CV1 V2 a a b b F1 F2 c c C(-1, -2) V(-9, -2), (8, -2) F(-6.7, -2), (4.7, -2)

Slide30CV1 V2 F1 F2 C(0, 0) V(-4, 0), (4, 0) F(-2.6, 0), (2.6, 0)

Slide33Now graph it………

Slide34CV1 V2 F1 F2 C(-3, 1) V(-7, 1), (1, 1) F(-5, -1), (-1, 1)

Slide35find the equation of the ellipse whose center is at (2, -2), vertexat (7, -2) and focus at (4, -2). C F V C(2, -2) a = 5 c = 2

Slide36find the equation of the ellipse with vertices at (4, 3) and (4, 9) ,and focus at (4, 8) V V C C(4, 6) a = 3 F c = 2

Slide37find the equation of the ellipse whose foci are (5, 1) and (-1, 1),and length of the major axis is 8 F F C C(2, 1) c = 3 Major is 8 Semi-major is 4 a = 4