Rumus Perbandingan Trigonometri untuk Sudut-sudut Berelasi 90 Derajat
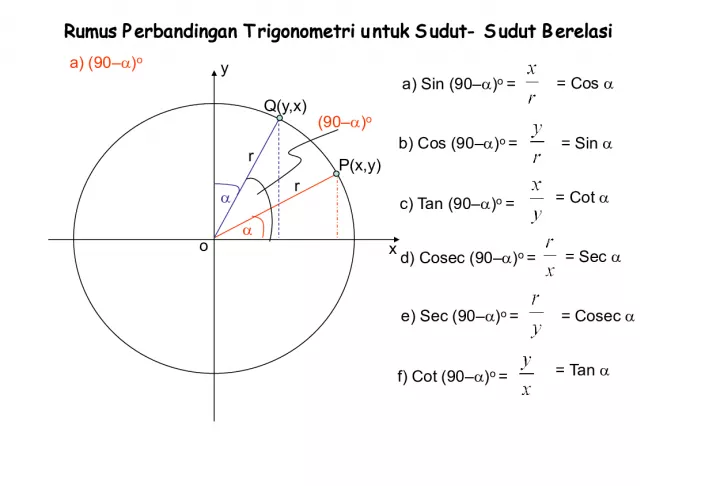

Dalam matematika, terdapat beberapa sudut yang berelasi dengan sudut 90
- Uploaded on | 2 Views
-
 anthony
anthony
About Rumus Perbandingan Trigonometri untuk Sudut-sudut Berelasi 90 Derajat
PowerPoint presentation about 'Rumus Perbandingan Trigonometri untuk Sudut-sudut Berelasi 90 Derajat'. This presentation describes the topic on Dalam matematika, terdapat beberapa sudut yang berelasi dengan sudut 90. The key topics included in this slideshow are . Download this presentation absolutely free.
Presentation Transcript
Slide1Ru m u s P e r b a n d i n g a n T r i g o n o m e t r i u n t u k S u d u t - S u d u t B e r e l a s i x y a) (90 – ) o a) Sin (90 – ) o = b) Cos (90 – ) o = c) Tan (90 – ) o = d) Cosec (90 – ) o = e) Sec (90 – ) o = f) Cot (90 – ) o = r o P(x,y) Q(y,x) r (90 – ) o = Cos = Sin = Cot = Sec = Cosec = Tan
Slide2rumus perbandingan trigonometri untuk sudut- sudut Berelasix y b ) ( 9 0 + ) o r o Q( –y ,x) = Cos = – Sin = – Cot = Sec = – Cosec = – Tan P(x,y) r a) Sin (90 + ) o = b) Cos (90 + ) o = c) Tan (90 + ) o = d) Cosec (90 + ) o = e) Sec (90 + ) o = f) Cot (90 + ) o = (90 + ) o
Slide3rumus perbandingan trigonometri untuk sudut- sudut Berelasix y b) (180 – ) o r o Q( – x,y) = – Cos = Sin = – Cot = – Sec = Cosec = – Tan P(x,y) r a) Sin (180 – ) o = b) Cos (180 – ) o = c) Tan (180 – ) o = d) Cosec (180 – ) o = e) Sec (180 – ) o = f) Cot (180 – ) o = (180 – ) o
Slide4Ca r a M e n g i n g a t n y a : 1 . D i a n g g a p S u d u t l a n c i p 2 . B e n t u k S u d u t t e r s e b u t p a d a k u a d r a n b e r a p a ? 3 . N i l a i f u n g s i t e r s e b u t ( + ) a t a u ( – ) i n g a t A l l S i n T a n C o s 4 . J i k a b e n t u k n y a ( 9 0 ± ) o a t a u ( 2 7 0 ± ) o M a k a F u n g s i B e r u b a h Sin Cos Tan Cot Sec Cosec U n t u k b e n t u k y a n g l a i n (180 ± ) o ( – ) (nx360 ± ) o F U N G S I T E T A P
Slide51. D i a n g g a p S u d u t l a n c i p 2 . B e n t u k S u d u t t e r s e b u t p a d a k u a d r a n b e r a p a ? 3 . N i l a i f u n g s i t e r s e b u t ( + ) a t a u ( – ) i n g a t A l l S i n T a n C o s 4 . J i k a b e n t u k n y a ( 9 0 ± ) o a t a u ( 2 7 0 ± ) o M a k a F u n g s i B e r u b a h S i n C o s Tan Cot Sec Cosec U n t u k b e n t u k y a n g l a i n ( 1 8 0 ± ) o ( – ) ( n x 3 6 0 ± ) o F U N G S I T E T A P Contoh Cos(90 + ) o = Sin – Sin(180 + ) o = – Sin Tan(180 + ) o = + Tan Sin ( – ) = – Sin Cos ( – ) = + Cos Cos(360 + ) o = + Cos Cos(270 + ) o = Sin + All + Cosec + Sin + Cos+ Sec + Cot + Tan +