Finding Increase and Decrease of a Function and Connecting it with its Derivative

Slide1DO NOW: Find where the function f(x) = 3x 4  – 4x 3  – 12x 2  + 5 is increasing and decreasing.

Slide2HW: Pg.4.3 – Connecting  f ’ and  f ’’ with the Graph of  f

Slide3First Derivative Test Recall that at a critical point, a function can have:  A local maximum,  A local minimum, or  Neither. We can look at whether f’ changes sign at the critical point to decide which of the above possibilities is the case:

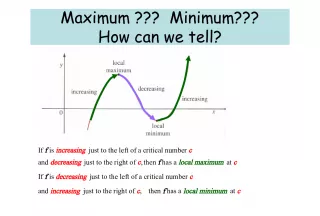
Slide4First Derivative Test (cont’d)The First Derivative Test    Suppose that c is a critical number of a continuous function f. (a) If f’ changes from positive to negative at c, then f has a local _____________ at c. (b) If f’ changes from negative to positive at c, then f has a local _____________ at c. (c) If f’ does not change sign at c (that is, f’ is positive on both sides of c or negative on both sides), then f has no local maximum or minimum at c.

Slide5Concavity In the figure on the next slide, the  Slopes of the tangent lines increase from left to right on the interval (a,b), and so A function (or its graph) is called  concave upward  on an interval  I  if i is an increasing function on  I .  It is called  concave downward  on  I  if f’ is decreasing on  I .

Slide6Concavity Concave ___________:  F’ is decreasing    f’’ < 0  Concave ___________:  F’ is increasing    f’’ > 0

Slide7Inflection Point A point where a curve changes its direction of concavity is called an inflection point.  Thus there is a point of inflection at any point where the second derivative changes sign. Concavity Test (a) If  f’’(x)  > 0 for all x in  I , then the graph of f is concave upward on  I . (b) If  f’’(x)  < 0 for all x in  I , then the graph of f is concave downward on  I .

Slide8Determining Local Max/MinThe Second Derivative Test    Suppose f’’ is continuous near c. (a) If f’(c) = 0 and f’’(c) > 0, then f has a local minimum at c. (b) If f’(c) = 0 and f’’(c) < 0, then f has a local maximum at c.

Slide9Example 1 Discuss y = x 4  – 4x 3  with respect to  Concavity,  Points of inflection, and  Local maxima and minima.

Slide10Example 1 (solution)

Slide11Example 2 Discuss f(x) = x 2/3 (6 – x) 1/3  with respect to:  Concavity  Points of inflection, and  Local maxima and minima.

Slide12Example 2 (solution)