Understanding Integers and Addition

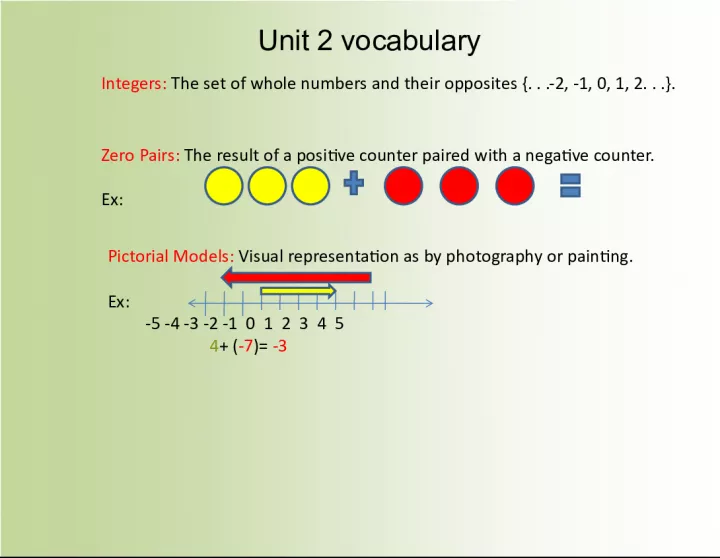
1. Integers: The set of whole numbers and their opposites {. . .-2, -1, 0, 1, 2. . .}. Zero Pairs: The result of a positive counter paired with a negative counter. Ex: Pictorial Models: Visual representation as by photography or painting. Ex: -5 -4 -3 -2 -1 0 1 2 3 4 5 4 + ( -7 )= -3 Unit 2 vocabulary

2. Adding Integers: When adding two positive integers the answer will always be positive. When adding two negative integers the answer will always be negative . When adding a positive and a negative integers the answer will keep the the sign of the larger number Sum: The addend is one of the numbers that is being added in order to find a sum. Additive inverse: A number that when added to a given number, results in a sum of zero. Example: The additive inverse of 4 is -4 because 4 + (-4) = 0.

3. Subtracting Integers: When subtracting positive integers the answer will be positive. When subtracting negative integers the answer will depend on the larger number Ex: -3-4=-7 or -3-(-4)=1 . When two negative signs are side by side they will change to a positive sign. . Difference: The difference is the answer in a subtraction problem. Example: 4 Minuend -1 Subtrahend 3 Difference

4. Multiplying Integers: When multiplying integers follow the rules of: + x + = + - X - = - + x - = - Factor: The factor of a number is a number that divides that number exactly. For example, the factors of 6 are 1, 2, 3 and 6. Product: The product is the answer in a multiplication problem. Example: 5 Multiplicand x 2 Multiplier 10 Product

5. Dividing integers: When dividing integers the same rules apply as multiplication. + x + = + - x - = - and + x - = - Divisor: is the number that the dividend is divided by (in long division ). Example: 6 ÷ 2 = 3 Dividend: is the number that is divided (in long division ). The dividend divided by the divisor is the quotient . Example: 6 ÷ 2 = 3 Quotient: is the answer in long division . The dividend divided by the divisor is the quotient . Example: 6 ÷ 2 = 3

6. Coordinate Plane: A plane, also called a coordinate grid or coordinate system, in which a horizontal number line and a vertical number line intersect at their zero points. X-Axis: The horizontal line on a coordinate plane. Y-Axis: The Vertical line on a Coordinate Plane Quadrant: A quadrant is a quarter of a plane . The x-axis and y-axis divide the x-y plane into four quadrants. The axes themselves are not part of the quadrants.

7. Ordered Pair: A pair of numbers used to locate a point in the coordinate plane or the solution of an equation in two variables. An ordered pair is written in the form: Ex. (3,2) ( x -coordinate, y -coordinate). Coordinates: are an ordered pair of numbers that show the location of a point on the x-y plane. Every point on the plane can be located by a pair of coordinates (x,y), which notes its distance from the x-axis and the y-axis . Respectively: in the order given Concrete: capable of being perceived by the senses; not abstract or imaginary; "concrete objects such as trees"

8. Line segment: the part of a line that is between two endpoints. Ex. ._________________. Endpoint: the point at the beginning and end of a line segment Ex. ._______________ . Midpoint: On a line segment, the point that is halfway between the endpoints. Ex. ._________._________.