Stability of Financial Models

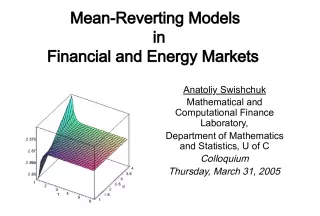
Slide1Stability of Financial ModelsAnatoliy Swishchuk Mathematical and Computational Finance Laboratory Department of Mathematics and Statistics University of Calgary, Calgary, Alberta, Canada E-mail:  aswish@math.ucalgary.ca Web page: http://www.math.ucalgary.ca/~aswish/ Talk ‘Lunch at the Lab’ MS543, U of C 25th November, 2004

Slide2Outline• Definitions of Stochastic Stability • Stability of Black-Scholes Model • Stability of Interest Rates: Vasicek, Cox- Ingersoll-Ross (CIR) • Black-Scholes with Jumps: Stability • Vasicek and CIR with Jumps: Stability

Slide3Why do we need the stability offinancial models?

Slide4Definitions of Stochastic Stability1)   Almost Sure  Asymptotical Stability of Zero State 2)  Stability in the  Mean  of Zero State 3) Stability in the  Mean Square  of Zero State 4)  p-Stability  in the Mean of Zero State Remark :  Lyapunov index  is used for 1) ( and also for 2), 3) and 4)): If then zero state is stable almost sure. Otherwise it is unstable.

Slide5Black-Scholes Model (1973)Bond Price Stock Price r>0-interest rate -appreciation rate >0-volatility Remark . Rendleman & Bartter (1980) used this equation to model interest rate

Slide6Ito Integral in Stochastic TermDifference between Ito calculus and classical (Newtonian calculus): 1)  Quadratic variation of differentiable function on [0,T] equals to 0: 2)  Quadratic variation of Brownian motion on [0,T] equals to T: In particular, the paths of Brownian motion are not differentiable .

Slide7Simulated Brownian Motion

Slide8Stability of Black-Scholes Model. I.Solution for Stock Price If ,  then  S t =0 is almost sure stable Idea : and almost sure Otherwise it is unstable

Slide9Stability of Black-Scholes Model. II.• p-Stability If then the  S t =0 is p-stable Idea:

Slide10Stability of Black-Scholes Model. III.• Stability of Discount Stock Price If then the  X  t =0 is almost sure stable Idea:

Slide11Black-Scholes with JumpsN  t-Poisson process with intensity moments of jumps independent identically distributed r. v. in On the intervals At the moments Stock Price with Jumps The sigma-algebras generated by ( W  t , t>=0), ( N  t, t>=0) and ( U  i; i>=1) are independent.

Slide12Simulated Poisson Process

Slide13Stability of Black-Scholes with Jumps. I.If ,  then  S t=0 is almost sure stable Idea: Lyapunov index

Slide14Stability of Black-Scholes with Jumps. II.If ,  then  S t =0 is p-stable . Idea: 1st step : 2nd step : 3d step :

Slide15Vasicek Model for Interest Rate (1977)Explicit Solution: Drawback :  P  ( r  t <0)>0,  which is not satisfactory from a practical point of view.

Slide16Stability of Vasicek ModelMean Value: Variance: since

Slide17Vasicek Model with JumpsN   t  -  Poisson process U   i  –  size of ith jump

Slide18Stability of Vasicek Model with JumpsMean Value: Variance: since

Slide19Cox-Ingersoll-Ross Model of InterestRate (1985) If then the process actually stays strictly positive. Explicit solution: b  t  is some Brownian motion, random time Otherwise, it is nonnegative

Slide20Stability of Cox-Ingersoll-Ross ModelMean Value : Variance: since

Slide21Cox-Ingersoll-Ross Model with JumpsN   t   is a Poisson process U  i   is size of ith jump

Slide22Stability of Cox-Ingersoll-Ross Model withJumps Mean Value : Variance : since

Slide23Conclusions• We considered Black-Scholes, Vasicek and Cox-Ingersoll-Ross models (including models with jumps) • Stability of Black-Scholes Model without and with Jumps • Stability of Vasicek Model without and with Jumps • Stability Cox-Ingersoll-Ross Model without and with Jumps • If we can keep parameters in these ways- the financial models and markets will be stable

Slide24Thank you for your attention!