Calculations of Solution Concentration

Slide1Calculations of Solution  Concentration Calculations  of Solution  Concentration

Slide2CA Standards CA  Standards

Slide3Calculations of  Solution  Concentration: Grams  per  Liter Calculations  of  Solution  Concentration: Grams  per  Liter Grams  per  liter   Grams  per  liter   is the ratio of mass units of solute to volume (liters) of solution

Slide4Calculations of  Solution  Concentration: Molarity Calculations  of  Solution  Concentration: Molarity Molarity Molarity  is the ratio of moles of solute to liters of solution

Slide5Calculations of  Solution  Concentration: Mass  Percent Calculations  of  Solution  Concentration: Mass  Percent Mass  percent   Mass  percent   is the ratio of mass units of solute to mass units of solution, expressed as a percent

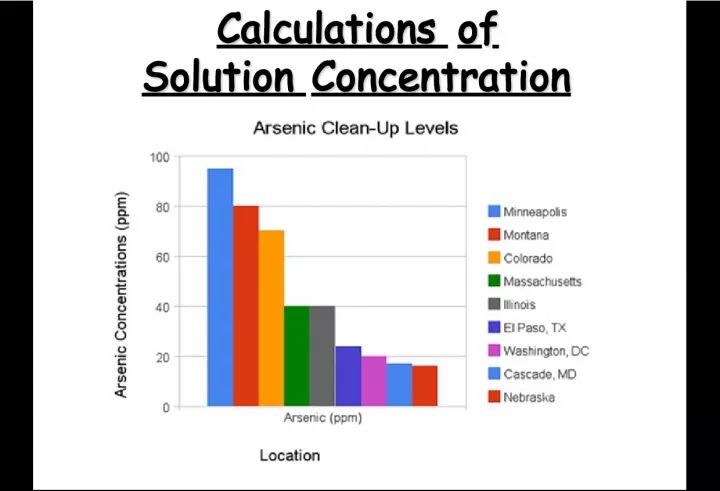
Slide6Calculations of  Solution  Concentration: Parts  per  Million Calculations  of  Solution  Concentration: Parts  per  Million Parts  per  million  Parts  per  million  is the ratio of mass units of solute to mass units of solution, multiplied by one million (10 6 )

Slide7A Simplifying  Assumption A  Simplifying  Assumption • 1  ml  of  water  =  1  gram  of  water • 1  ml  of  water  =  1  gram  of  water • 1000  ml  of  water  =  1  liter  =  1000 grams • 1000  ml  of  water  =  1  liter  =  1000 grams • Assume   that  solutions  with  water  as the  solvent  have  the  density  of pure  water  (1  mL  =  1  gram) • Assume   that  solutions  with  water  as the  solvent  have  the  density  of pure  water  (1  mL  =  1  gram) – It’s  not  true,  but  it’s  close enough   – It’s  not  true,  but  it’s  close enough  