Perbandingan Trigonometri Sudut-sudut di Semua Kuadran

Artikel ini membahas tentang perbandingan trigonometri dari sin, cos, tan, cot, cosec, dan
- Uploaded on | 0 Views
-
 doenja
doenja
About Perbandingan Trigonometri Sudut-sudut di Semua Kuadran
PowerPoint presentation about 'Perbandingan Trigonometri Sudut-sudut di Semua Kuadran'. This presentation describes the topic on Artikel ini membahas tentang perbandingan trigonometri dari sin, cos, tan, cot, cosec, dan. The key topics included in this slideshow are . Download this presentation absolutely free.
Presentation Transcript
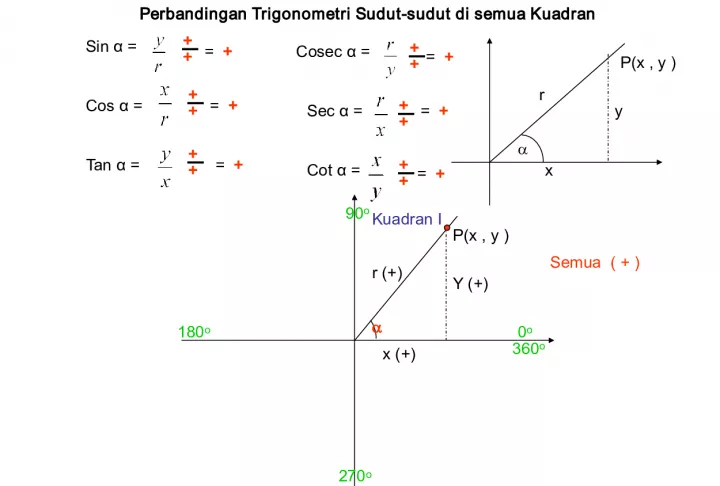
Slide1Pe r b a n d i n g a n T r i g o n o m e t r i S u d u t - s u d u t d i s e m u a K u a d r a n S i n α = C o s α = T a n α = C o t α = C o s e c α = S e c α = P(x , y ) x r y P(x , y ) Kuadran I Y (+) x (+) r (+) + + = + + + = + = + + + + + + + + + = + = + = + Semua ( + ) 360 o 0 o 90 o 180 o 270 o
Slide2perbandingan trigonometri sudut-sudut di semua kuadranSin α = Cos α = Tan α = Cot α = Cosec α = Sec α = Kuadran II Semua ( + ) P(x , y ) r (+) y (+) x ( - ) + + = + _ + + + = + = ─ = ─ ─ + ─ + = ─ = ─ _ + Sin α = (+) Cosec α = (+) Kuadran I 360 o 0 o 90 o 180 o 270 o
Slide3perbandingan trigonometri sudut-sudut di semua kuadranSin α = Cos α = Tan α = Cot α = Cosec α = Sec α = Semua ( + ) = ─ ─ – _ + = + Kuadran III Cosec α = (+) Sin α = (+) Y ( – ) r (+) P(x , y ) x ( – ) ─ + = ─ _ + = ─ ─ + = ─ ─ – = + Tan α = (+) Cot α = (+) Kuadran II Kuadran I 360 o 0 o 90 o 180 o 270 o
Slide4perbandingan trigonometri sudut-sudut di semua kuadranSin α = Cos α = Tan α = Cot α = Cosec α = Sec α = Semua ( + ) Tan α = (+) Cot α = (+) Cosec α = (+) Sin α = (+) Kuadran IV P(x , y ) x (+) r (+) _ + Y ( – ) = ─ = + ─ + = ─ + + + + = + _ + = ─ ─ + = ─ Kuadran III Kuadran II Kuadran I Cos α = (+) Sec α = (+) 360 o 0 o 90 o 180 o 270 o
Slide5Ca r a m e n g i n g a t n y a : “ A l l S i n T a n C o s “ Artinya : D i k u a d r a n I S e m u a n y a b e r n i l a i p o s i t i f D i k u a d r a n I I S i n d a n C o s e c b e r n i l a i p o s i t i f D i k u a d r a n I I I T a n d a n C o t b e r n i l a i p o s i t i f D i k u a d r a n I V C o s d a n S e c b e r n i l a i p o s i t i f
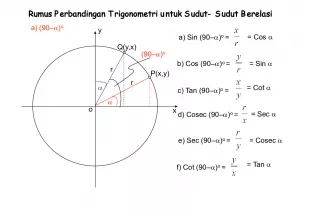
Slide6Ru m u s P e r b a n d i n g a n T r i g o n o m e t r i u n t u k S u d u t - S u d u t B e r e l a s i x y a) (90 – ) o a) Sin (90 – ) o = b) Cos (90 – ) o = c) Tan (90 – ) o = d) Cosec (90 – ) o = e) Sec (90 – ) o = f) Cot (90 – ) o = r o P(x,y) Q(y,x) r (90 – ) o = Cos = Sin = Cot = Sec = Cosec = Tan
Slide7rumus perbandingan trigonometri untuk sudut- sudut Berelasix y b ) ( 9 0 + ) o r o Q( –y ,x) = Cos = – Sin = – Cot = Sec = – Cosec = – Tan P(x,y) r a) Sin (90 + ) o = b) Cos (90 + ) o = c) Tan (90 + ) o = d) Cosec (90 + ) o = e) Sec (90 + ) o = f) Cot (90 + ) o = (90 + ) o
Slide8rumus perbandingan trigonometri untuk sudut- sudut Berelasix y b) (180 – ) o r o Q( – x,y) = – Cos = Sin = – Cot = – Sec = Cosec = – Tan P(x,y) r a) Sin (180 – ) o = b) Cos (180 – ) o = c) Tan (180 – ) o = d) Cosec (180 – ) o = e) Sec (180 – ) o = f) Cot (180 – ) o = (180 – ) o
Slide9Ca r a M e n g i n g a t n y a : 1 . D i a n g g a p S u d u t l a n c i p 2 . B e n t u k S u d u t t e r s e b u t p a d a k u a d r a n b e r a p a ? 3 . N i l a i f u n g s i t e r s e b u t ( + ) a t a u ( – ) i n g a t A l l S i n T a n C o s 4 . J i k a b e n t u k n y a ( 9 0 ± ) o a t a u ( 2 7 0 ± ) o M a k a F u n g s i B e r u b a h Sin Cos Tan Cot Sec Cosec U n t u k b e n t u k y a n g l a i n (180 ± ) o ( – ) (nx360 ± ) o F U N G S I T E T A P
Slide101. D i a n g g a p S u d u t l a n c i p 2 . B e n t u k S u d u t t e r s e b u t p a d a k u a d r a n b e r a p a ? 3 . N i l a i f u n g s i t e r s e b u t ( + ) a t a u ( – ) i n g a t A l l S i n T a n C o s 4 . J i k a b e n t u k n y a ( 9 0 ± ) o a t a u ( 2 7 0 ± ) o M a k a F u n g s i B e r u b a h S i n C o s Tan Cot Sec Cosec U n t u k b e n t u k y a n g l a i n ( 1 8 0 ± ) o ( – ) ( n x 3 6 0 ± ) o F U N G S I T E T A P Contoh Cos(90 + ) o = Sin – Sin(180 + ) o = – Sin Tan(180 + ) o = + Tan Sin ( – ) = – Sin Cos ( – ) = + Cos Cos(360 + ) o = + Cos Cos(270 + ) o = Sin + All + Cosec + Sin + Cos+ Sec + Cot + Tan +