Optimal Blocking of Orthogonal Arrays in Designed Experiments

1. Optimal Blocking of Orthogonal Arrays in Designed Experiments Peter Goos

2. Optimal Blocking of Orthogonal Arrays in Designed Experiments Peter Goos In collaboration with Eric Schoen and Bagus Sartono

3. Factorial experiments - Treatments are described by combinations of factor levels - Interest is in main effects and two-factor interaction effects Experimental tests or runs need to be partitioned in blocks (due to different days, batches of raw material, ) Block effects are treated as fixed Experimenting is expensive, so we have small data ! Starting point

4. 1. Many processes have sources of variability that are uncontrollable. 2. Examples are day-to-day variation, batch-to- batch variation, etc. 3. When experimenting, this leads to groups of observations. 4. The groups are called blocks . 5. The grouping variable (day, batch) is called a blocking factor . 6. Responses within each group are more homogeneous or similar than responses from different groups. Experiments in blocks

5. PART 1: the number of observations exceeds the number of main effects and two-factor interactions - Vitaming stability experiment - 32 observations (8 blocks of size 4) - 64 observations (16 blocks of size 4) PART 2: the number of observations is too small to estimate all two-factor interaction effects Outline

6. Model of interest (in case all factors have 2 levels)

7. PART 1 The number of runs is big enough to estimate all main effects and two-factor interactions. Focus on 2-level factors n 1 + k + k(k 1)/2

8. I have always advocated optimal design of experiments - Flexible in terms of numbers of runs - Different types of factors - Constraints on the factor levels - - Implicitly assuming that `traditional designs do a good job when the number of observations is a power of 2 or a multiple of 4 Today, I start talking about situations where n is a power of 2, as well as the number of blocks Context

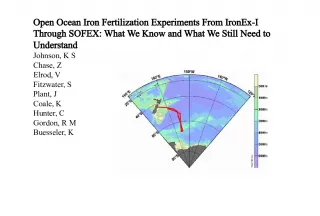
9. Vitamins degrade when exposed to light Can be stabilized when embedded in a special molecule, called a fatty molecule Five different fatty molecules Binding with sugar might help as well to stabilize the vitamins Experiment involving 6 two-level factors Vitamin stability experiment

10. 1. Boundedness with sugar. 2. Oil Red O. 3. Oxybenzone. 4. Beta Carotene. 5. Sulisobenzone 6. Deoxybenzone Six factors Fatty molecules

11. Vitamins degrade when exposed to light Can be stabilized when embedded in a special molecule, called a fatty molecule Five different fatty molecules Binding with sugar might help as well to stabilize the vitamins Experiment involving 6 two-level factors Vitamin stability experiment

12. Vitamins degrade when exposed to light Can be stabilized when embedded in a special molecule, called a fatty molecule Five different fatty molecules Binding with sugar might help as well to stabilize the vitamins Experiment involving 6 two-level factors There is day-to-day variation in the process Vitamin stability experiment

13. Vitamins degrade when exposed to light Can be stabilized when embedded in a special molecule, called a fatty molecule Five different fatty molecules Binding with sugar might help as well to stabilize the vitamins Experiment involving 6 two-level factors There is day-to-day variation in the process 4 runs per day are possible 8 days are available Vitamin stability experiment

14. Vitamin stability experiment 6 two-level factors 8 days of 4 runs or observations 32 runs in total model - 6 main effects - 15 two-factor interaction effects - 1 intercept - 7 contrasts for the 8-level blocking factor - 29 parameters in total

15. Traditional design approach Table 4B.3 in Wu & Hamada (2 6-1 design)

17. Traditional approach Design generator 6=12345 to choose 32 treatments or factor level combinations Block generators to arrange 32 runs in 8 blocks of 4 runs - B 1 = 135 - B 2 = 235 - B 3 = 145

18. 32-run orthogonal design

19. Traditional approach Perfect design for main effects - Can be estimated independently, with maximum precision - Estimates not affected by day-to-day variation - No variance inflation - No multicollinearity Not so for interaction effects - 12 of the 15 interactions can be estimated independently, with maximum precision - 3 interaction effects (12, 34, 56) cannot be estimated - Perfect collinearity with the blocks

20. Traditional approach (bis) Double the number of runs ! 64 instead of 32 runs Full factorial design instead of half fraction 16 blocks of size 4 Table 3A in Wu & Hamada (2000)

22. Traditional approach (bis) Block generators to arrange 64 runs in 16 blocks of 4 runs - B 1 = 136 - B 2 = 1234 - B 3 = 3456 - B 4 = 123456 We can estimate all two-factor interaction effects except 12, 34 and 56

23. Conclusion The 64-run design is a waste of resources. The traditional approach doesnt work.

24. Semi-traditional approach 64 observations in 16 blocks of size 4 Do not start from full factorial design ! Instead, cleverly combine two half fractions of 32 observations arranged in 8 blocks of size 4

25. First half fraction Design generator 6=12345 to choose 32 treatments or factor level combinations Block generators to arrange 32 observations in 8 blocks of 4 runs - B 1 = 135 - B 2 = 235 - B 3 = 145 We can estimate all two-factor interaction effects except 12, 34 and 56 This was the original idea

26. Second half fraction Design generator 6= 12345 to choose 32 treatments or factor level combinations Block generators to arrange 32 observations in 8 blocks of 4 runs - B 1 = 135 124 - B 2 = 235 134 - B 3 = 145 125 We can estimate all two-factor interaction effects except 23 , 45 and 16

27. Semi-traditional approach Result is a full factorial design From the first half of the experiment, we cannot estimate 12, 34 and 56 But we can estimate these effects from the second half From the second half of the experiment, we cannot estimate 23, 45 and 16 But we can estimate them from the first half

28. Semi-traditional approach

29. Some similar scenarios 5 two-level factors, 32 runs, 8 blocks of size 4: better to use two (cleverly selected) half fractions than it is to use a full factorial design 6 two-level factors, 64 runs, 16 blocks of size 4: - better to use two 32-run half fractions than to use a full factorial - but you can also combine a 32-run half fraction with a 16-run quarter fraction !

30. Advice to experimenters Do not trust tables in DOE textbooks ! Do not trust options for screening designs in your favorite software !

31. Advice to DOE textbook writers Make clear that certain designs in the tables should not be used ! And describe the better alternatives.

32. Advice to DOE software developers Make clear that certain screening design options should not be used ! And provide the better alternatives.

33. Advice to experimenters Do not trust tables in DOE textbooks ! Do not trust options for screening designs in your favorite software !

34. Advice to experimenters Throw away the DOE textbooks ! Do not trust options for screening designs in your favorite software !

35. Advice to experimenters Throw away the DOE textbooks ! Use optimal design of experiments !

36. D-optimal design I Calculate a 64-run D-optimal design with 16 blocks of size 4 Main effects + two-factor interactions Really easy with SAS, JMP, Design Expert, D-optimal design is 3% better than the design produced by the semi-traditional approach Design is not orthogonally blocked

37. D-optimal design I

38. D-optimality criterion: seeks designs that maximize determinant of information matrix Algorithms by Atkinson & Donev (1989) and Cook and Nachtsheim (1989) I used JMPs coordinate-exchange algorithm Optimal design

39. This is interesting but it does not solve the original problem which was to find a 32-run two-level design in 8 blocks of size 4 for estimating main effects and two-factor interaction effects

40. D-optimal design II Calculate a 32-run D-optimal design with 8 blocks of size 4 Main effects + two-factor interactions Really easy with SAS, JMP, Design Expert, All 2fis are estimable Design is not orthogonally blocked VIFs range from 1 to 2.6 only

41. D-optimal design II

42. Traditional design

43. 42 Conclusion Part 1 64 runs 64-run textbook design was beaten by manually constructed design manually constructed design was beaten by optimal design 32-run textbook design was beaten by optimal design So, optimal designs do a better job than classical designs even in scenarios that are ideal for classical designs

44. PART 2 The number of runs is not big enough to estimate all main effects and two-factor interactions. Optimal design approach not feasible since information matrix is singular in that case. Factors with 2, 3 and 4 levels

45. 44 Orthogonal arrays There exist many orthogonal arrays (OAs) that can be used as an experimental design 2-level arrays Regular full and fractional factorial designs Plackett-Burman designs Other nonregular arrays 3-level arrays: regular full and fractional factorial designs, nonregular arrays Mixed-level arrays: not all factors have the same number of levels (e.g. Taguchis L18)

46. 45 Strength-2 (or resolution-III) arrays Main effects can be estimated independently from each other But they are aliased with two-factor interactions Using complete catalogs of OAs, we sought optimal blocking patterns based on the concept of generalized word-length pattern Orthogonal blocking for main effects As little aliasing and confounding for two- factor interactions as possible We listed optimally blocked designs with 12, 16, 20, 24 and 27 runs

47. 46 20 runs, eight 2-level factors, five blocks Blocks 00001111222233334444 ----- -- ------------- ------------------ X1 00110011001100110011 X2 00110101010101011100 X3 00110110101011000101 X4 00111001110010100110 X5 01010011011011001010 X6 01010101100110101001 X7 01011010010101100101 X8 01011100001110010110

48. 47 27 runs, nine 3-level factors, nine blocks Blocks 000111222333444555666777888 -------- -- ---------------------------------------- X1 012012012012012012012012012 X2 012012012120120120201201201 X3 012012012201201201120120120 X4 012120201012120201012120201 X5 012120201120201012201012120 X6 012120201201012120120201012 X7 012201120012201120120012201 X8 012201120120012201012201120 X9 012201120201120012201120012

49. 48 Strength-3 (or resolution IV) arrays Main effects can be estimated independently From each other From two-factor interaction effects Two-factor interactions are aliased with each other Enumerating all possible blocking patterns for all OAs in catalogs was infeasible We used mixed integer linear programming instead to find blocking arrangements of good orthogonal arrays: Orthogonally blocked for main effects As little confounding between two-factor interactions and blocks as possible

50. 49 Mixed integer linear programming Input: A good OA which allows estimation of many two-factor interactions Number of blocks required Output: Optimal blocking pattern (orthogonal for the main effects) Tells you when it is infeasible to find such a pattern Implementations SAS/OR Matlab + CPLEX

51. 50 40 runs, one 5-level factor, six 2-level factors, four blocks 0 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0 0 1 1 1 2 0 1 1 0 1 1 1 2 1 0 1 0 0 0 1 3 0 0 1 1 1 0 1 3 0 1 0 0 1 1 1 4 0 1 0 0 0 0 1 4 1 1 1 1 0 1 1 --------------------------------------------------------- 0 0 1 1 1 1 0 2 0 1 1 0 1 0 1 2 1 1 0 1 1 1 1 2 1 1 1 1 0 0 0 2 2 0 0 0 0 1 0 2 2 0 0 1 1 0 1 2 3 0 1 1 0 0 0 2 3 1 0 0 0 1 0 2 4 0 1 0 1 1 1 2 4 1 0 0 0 0 1 2 --------------------------------------------------------- 0 0 0 0 0 0 0 3 0 1 0 1 0 1 1 3 1 0 0 1 0 1 0 3 1 0 1 1 1 0 1 3 2 0 1 0 1 0 0 3 2 1 1 0 0 0 1 3 3 0 0 0 1 0 1 3 3 1 1 1 1 1 1 3 4 1 0 0 1 1 0 3 4 1 1 1 0 1 0 3 --------------------------------------------------------- 0 0 1 1 0 0 1 4 0 1 1 0 0 1 0 4 1 0 0 0 0 0 1 4 1 0 1 0 1 1 0 4 2 1 0 0 1 1 1 4 2 1 1 1 1 1 0 4 3 1 0 1 0 0 1 4 3 1 1 0 1 0 0 4 4 0 0 1 0 1 1 4 4 0 0 1 1 0 0 4

52. 51 Conclusion Part 2 Catalogs of orthogonal arrays offer a starting point for designing blocked experiments For small numbers of observations, it is possible to completely enumerate all possible designs and select the best For larger numbers of observations, a mixed integer linear programming approach can be used to arrange an appropriate orthogonal array in blocks

53. Based on Sartono, B., Goos, P., Schoen, E.D. (2014) Blocking Orthogonal Designs with Mixed Integer Linear Programming, Technometrics 56, to appear. Schoen E.D., Sartono B., Goos, P. (2013) Optimum blocking for general resolution-3 designs, Journal of Quality Technology 45, 166-187. Goos, P., Jones, B. (2011) Optimal Design of Experiments: A Case-Study Approach, Wiley.

54. Optimal Blocking of Orthogonal Arrays in Designed Experiments Peter Goos In collaboration with Eric Schoen, Bagus Sartono and Nha Vo-Thanh