Logarithm Solving Tips

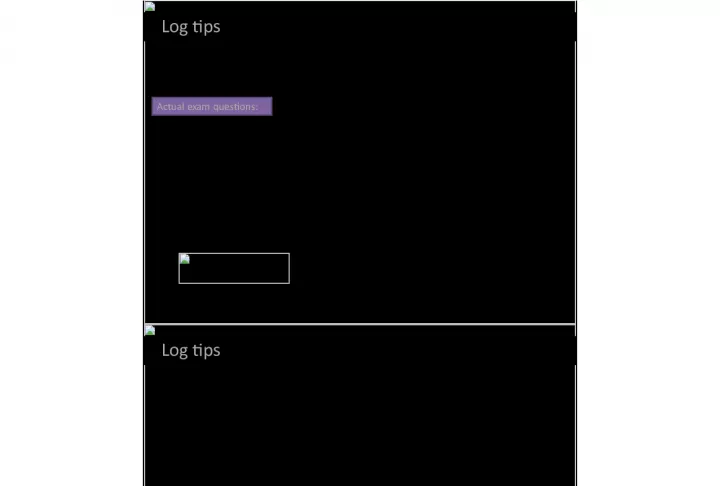
1. Solve log 2 (2 x + 1) log 2 x = 2 Log tips When solving, you can often either: a) Get in the form log a b = c . Then rearrange as a c = b b) Get in the form log a b = log a c . Then b = c. Actual exam questions: log 2 ( x + 1) log 2 x = log 2 7 2 log 3 x log 3 7 x = 1 Solve simultaneous equations: a = 3 b , log 3 a + log 3 b = 2 log 5 (4 x ) 2 log 5 x = 1 log 2 y = 3 log 2 (11 6 x ) = 2 log 2 ( x 1) + 3 log x 64 = 2

2. Log tips Other types of question: 3 x = 10 5 2 x 12(5 x ) + 35 = 0 What if you had 5 2x+1 here instead?

3. The points A and B have coordinates (2, 11) and (8, 1) respectively. Given that AB is a diameter of the circle C , ( a ) show that the centre of C has coordinates (3, 6), (1) ( b ) find an equation for C . (4) ( c ) Verify that the point (10, 7) lies on C . (1) ( d ) Find an equation of the tangent to C at the point (10, 7), giving your answer in the form y = mx + c , where m and c are constants. (4) Circles Remember that you need the centre (a,b) and the radius r, which gives the equation: (x-a) 2 + (y-b) 2 = r 2 The tangent is perpendicular to the radius at the point of contact.

4. Circles How could you tell if a line and a circle intersect: 0 times twice once Equate the expressions then look at the discriminant: b 2 4ac < 0 b 2 4ac > 0 b 2 4ac = 0 ? ? ? x 2 + y 2 = 1 y = 4-x

5. 8. The circle C , with centre at the point A , has equation x 2 + y 2 10 x + 9 = 0. Find ( a ) the coordinates of A , (2) ( b ) the radius of C , (2) ( c ) the coordinates of the points at which C crosses the x -axis. (2) Given that the line l with gradient is a tangent to C , and that l touches C at the point T , ( d ) find an equation of the line which passes through A and T . (3) Circles

6. Circles If PR is the diameter, how would you prove that a = 13?

7. Circles

8. Circles

9. ( a ) Use the factor theorem to show that ( x + 4) is a factor of 2 x 3 + x 2 25 x + 12. (2) ( b ) Factorise 2 x 3 + x 2 25 x + 12 completely. (4) Factor Theorem f( x ) = x 3 + ax 2 + bx + 3, where a and b are constants. Given that when f ( x ) is divided by ( x + 2) the remainder is 7, (a) show that 2 a b = 6 (2) Given also that when f ( x ) is divided by ( x 1) the remainder is 4, (b) find the value of a and the value of b. (4)

10. ( a ) Find all the values of , to 1 decimal place, in the interval 0 < 360 for which 5 sin ( + 30 ) = 3. (4) ( b ) Find all the values of , to 1 decimal place, in the interval 0 < 360 for which tan 2 = 4. (5) ( a ) Given that sin = 5 cos , find the value of tan . (1) ( b ) Hence, or otherwise, find the values of in the interval 0 < 360 for which sin = 5 cos , giving your answers to 1 decimal place. (3) Trigonometric Solutions Find all the solutions, in the interval 0 x < 2 , of the equation 2 cos 2 x + 1 = 5 sin x , giving each solution in terms of .

11. ( a ) Sketch, for 0 x 2 , the graph of y = sin ( x + ( /6)). (2) ( b ) Write down the exact coordinates of the points where the graph meets the coordinate axes. (3) ( c ) Solve, for 0 x 2 , the equation sin (x + ( /6)) = 0.65, giving your answers in radians to 2 decimal places. Solve, for 0 x < 360, ( a ) sin( x 20 ) = 1/ 2, (4) ( b ) cos 3 x = 1/2 . (6) Trigonometric Solutions ( a ) Show that the equation 3 sin 2 2 cos 2 = 1 can be written as 5 sin 2 = 3. (2) ( b ) Hence solve, for 0 < 360 , the equation 3 sin 2 2 cos 2 = 1, giving your answer to 1 decimal place. (7)

12. ( a ) Show that the equation 4 sin 2 x + 9 cos x 6 = 0 can be written as 4 cos 2 x 9 cos x + 2 = 0. (2) ( b ) Hence solve, for 0 x < 720, 4 sin 2 x + 9 cos x 6 = 0, giving your answers to 1 decimal place. (6) Show that the equation tan 2 x = 5 sin 2x can be written in the form (1 5 cos 2 x) sin 2x = 0 (2) (b) Hence solve, for 0 x 180, tan 2 x = 5 sin 2x giving your answers to 1 decimal place where appropriate. You must show clearly how you obtained your answers. (5) Trigonometric Solutions (i) Find the solutions of the equation sin(3x - 15 ) = for which 0 x 180

13. Trigonometric Solutions Summary of tips: To get all your solutions when you do you inverse sin/cos/tan: Remember that sin(180-x) = sin(x) and cos(360-x) = cos(x) sin and cos repeat every 360 (i.e. you can add 360 to your solution as many times as you like). But tan repeats every 180 . If youre working in radians, then sin(pi x) = sin(x), etc. Look at the range the question gives : if its in radians, give your answers in radians. Ensure your calculator is correctly set to either radians or degrees mode . If you have sin 2 , then make sure you get both positive and negative solution . Likewise for cos 2 and tan 2 . Make sure you write out enough solutions before you start manipulating: if you had sin(3x) = for example and had the range 0 < x < 360, then youd initially need to write values up to 1080 since youre going to be dividing by 3.

14. Areas of sector/Arc lengths/Sine and Cosine Rule

15. Areas of sector/Arc lengths/Sine and Cosine Rule

16. Areas Only 1 in 36 candidates (across the country) got this question fully correct.

17. Optimisation

18. Optimisation

19. Optimisation

20. Optimisation

21. Integration

22. Integration

23. Integration

24. Integration Examiners Report: (a) A pleasing majority of the candidates were able to differentiate these fractional powers correctly, but a sizeable group left the constant term on the end. They then put the derivative equal to zero. Solving the equation which resulted caused more problems as the equation contained various fractional powers. Some tried squaring to clear away the fractional powers, but often did not deal well with the square roots afterwards. There were many who expressed 6 x -1/2 = 1/(6 x 1/2 ) and tended to get in a muddle after that. Those who took out a factor x 1/2 usually ended with x = 0 as well as x = 4 and if it was not discounted, they lost an accuracy mark. Those who obtained the solution x = 4 sometimes neglected to complete their solution by finding the corresponding y value. Some weaker candidates did not differentiate at all in part (a), with some integrating, and others substituting various values into y. ?

25. Geometric Series

26. Geometric Series

27. Geometric Series

28. Binomial Expansion